Lattices
We include a class called LatticeOfFlats, which is associated with a hyperplane arrangement. This class keeps track of basic information we need to compute the various generating functions associated with a hyperplane arrangement. (For non-central arrangements, this is indeed not a lattice, but a semi-lattice.) All other functions are tied to the LatticeOfFlats class and, thus, are either attributes or methods. Methods are written as .method_name.
LatticeOfFlats
Input:
A=None: a hyperplane arrangement;poset=None: a graded poset with a bottom element;flat_labels=None: a dictionary from the elements of the poset to subsets of atoms;hyperplane_labels=None: a dictionary from the atoms of the poset to the hyperplanes;matroid=None: a matroid.
Output:
- the lattice of flats for the given hyperplane arrangement or matroid. If a poset is given, then the poset is returned.
Despite the name "lattice of flats" the underlying poset need not be a lattice.
Unless the poset and labels have been computed before, they should not be given as this function may compute the intersection poset of a hyperplane arrangement faster than the default in SageMath. It is not required to provide a hyperplane arrangement; in particular, one may instead only provide a matroid.
Attributes
The lattice of flats has four attributes:
hyperplane_arrangement: the given hyperplane arrangement;poset: the intersection poset;flat_labels: the dictionary indexed by the elements ofposetwith values given by subsets of the atoms ofposet;hyperplane_labels: the dictionary indexed by the atoms ofposetwith values equal to the hyperplanes ofhyperplane_arrangement.
Example (Lattice of braid arrangement)
We construct the lattice of flats for the braid arrangement in $\mathbb{R}^4$.
sage: A = hi.CoxeterArrangement("A3")
sage: A
Arrangement of 6 hyperplanes of dimension 4 and rank 3
sage: L = hi.LatticeOfFlats(A)
sage: L
The lattice of flats of:
Arrangement of 6 hyperplanes of dimension 4 and rank 3
given by:
Finite poset containing 15 elements
Now we look at the data stored in the attributes. We display the hyperplanes in the arrangement.
sage: L.hyperplane_arrangement
Arrangement of 6 hyperplanes of dimension 4 and rank 3
sage: L.hyperplane_arrangement.hyperplanes()
(Hyperplane 0*x0 + 0*x1 + x2 - x3 + 0,
Hyperplane 0*x0 + x1 - x2 + 0*x3 + 0,
Hyperplane 0*x0 + x1 + 0*x2 - x3 + 0,
Hyperplane x0 - x1 + 0*x2 + 0*x3 + 0,
Hyperplane x0 + 0*x1 - x2 + 0*x3 + 0,
Hyperplane x0 + 0*x1 + 0*x2 - x3 + 0)
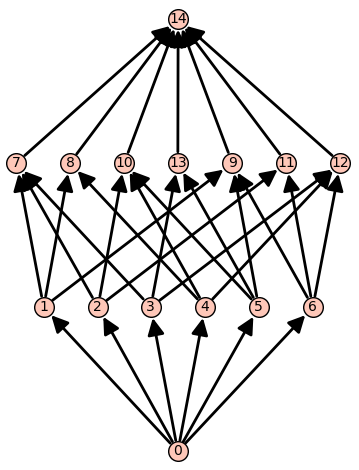
We display the poset as an image.
sage: L.poset
Finite poset containing 15 elements
Instead of showing the entire dictionaries, we will evaluate them at a few points.
sage: L.flat_labels[3]
{3}
sage: L.flat_labels[13]
{3, 5}
sage: L.flat_labels[9]
{1, 5, 6}
sage: L.flat_labels[0]
{}
We see that hyperplanes 1, 5, and 6 intersect in a codimension 2 subspace.
sage: L.hyperplane_labels[1]
Hyperplane 0*x0 + 0*x1 + x2 - x3 + 0
sage: L.hyperplane_labels[5]
Hyperplane x0 + 0*x1 - x2 + 0*x3 + 0
sage: L.hyperplane_labels[6]
Hyperplane x0 + 0*x1 + 0*x2 - x3 + 0
.atoms
Output:
- the atoms of the underlying poset.
.deletion
Input:
- a hyperplane $H$.
Output:
- the lattice of flats associated to the arrangement without $H$.
Example (Deletion in the braid arrangement)
We continue the $\mathsf{A}_3$ example started above. We will delete the hyperplane labeled by $2$ and display the resulting lattice of flats.
sage: L.deletion(2)
The lattice of flats of:
Arrangement of 5 hyperplanes of dimension 4 and rank 3
given by:
Finite poset containing 13 elements

.labels_of_flats
Output:
- the list of tuples with first entry an element of the poset and second entry a subset of atoms.
.labels_of_hyperplanes
Output:
- the list of tuples with first entry an element of the poset and second entry a hyperplane.
.Poincare_polynomial
Output:
- the Poincaré polynomial of the hyperplane arrangement.
.proper_part_poset
Output:
- the subposet without $\hat{0}$ and $\hat{1}$.
.show
No output given. This displays the underlying intersection poset using the default options in SageMath. This is a shortcut for L.poset.show().
.subarrangement
Input:
- an integer $x$.
Output:
- the lattice of flats of the interval $[\hat{0}, x]$.
Example (Subarrangement of the braid arrangement)
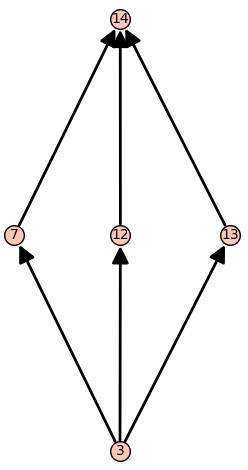
We continue from the original $\mathsf{A}_3$ example started above. We will construct the subarrangement from the flat labeled $10$.
sage: L.subarrangement(10)
The lattice of flats of:
Arrangement <x1 - x2 | x0 - x1 | x0 - x2>
given by:
Finite poset containing 5 elements
.restriction
Input:
- an integer $x$.
Output:
- the lattice of flats of the restriction to $x$ in the poset.
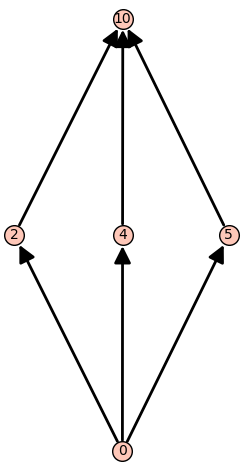
Example (Subarrangement of the braid arrangement)
We continue from the original $\mathsf{A}_3$ example started above. We will construct the restriction from the flat labeled $3$.
sage: L.restriction(3)
The lattice of flats of:
Arrangement <-x0 + x1 | x1 | x0>
given by:
Finite poset containing 5 elements